这不是一个完整的笔记，而是作为一个 attached link 附在 Zotero 上以做补充。

使用的教材：
https://github.com/MathFoundationRL/Book-Mathematical-Foundation-of-Reinforcement-Learning/tree/main

Bellman equation

关于式 2.7 的一些解释。

数学

这两个式子相等，是因为它们本质上是对同一组项进行求和，只是交换了求和的顺序。

在数学中，对于有限项的（或者绝对收敛的）双重求和，求和的顺序是可以任意交换的，这基于加法的交换律和结合律。

1. 第一个式子：

$\sum_{s' \in S} v_\pi(s') \sum_{a \in A} p(s'|s, a)\pi(a|s)$

我们看内部的和 $\sum_{a \in A} \dots$ 。$v_\pi(s’)$ 位于这个和的外部。
由于 $v_\pi(s’)$ 不依赖于求和变量 $a$，我们可以将其移到内部求和的里面（把它当作一个系数）： $\sum_{s' \in S} \left( \sum_{a \in A} v_\pi(s') p(s'|s, a)\pi(a|s) \right)$
现在，这就是一个标准的双重求和。它在对所有 $s’ \in S$ 和 $a \in A$ 的组合进行求和，求和的项是 $v_\pi(s’) p(s’|s, a)\pi(a|s)$。

2. 第二个式子：

$\sum_{a \in A} \pi(a|s) \sum_{s' \in S} p(s'|s, a)v_\pi(s')$

我们看内部的和 $\sum_{s’ \in S} \dots$ 。$\pi(a|s)$ 位于这个和的外部。
由于 $\pi(a|s)$ 不依赖于求和变量 $s’$，我们也可以将其移到内部求和的里面： $\sum_{a \in A} \left( \sum_{s' \in S} \pi(a|s) p(s'|s, a)v_\pi(s') \right)$
根据乘法交换律，求和的项 $\pi(a|s) p(s’|s, a)v_\pi(s’)$ 与第一个式子中的项 $v_\pi(s’) p(s’|s, a)\pi(a|s)$ 是完全相同的。
所以，这同样是一个双重求和，它也在对所有 $s’ \in S$ 和 $a \in A$ 的组合进行求和。

结论：

两个式子实际上都在计算同一个总和：

$\sum_{s' \in S} \sum_{a \in A} \left( v_\pi(s') p(s'|s, a)\pi(a|s) \right) = \sum_{a \in A} \sum_{s' \in S} \left( v_\pi(s') p(s'|s, a)\pi(a|s) \right)$

这就像计算一个表格中所有数字的总和：

第一个式子是“先按行求和，再把每行的结果加起来”。
第二个式子是“先按列求和，再把每列的结果加起来”。

在强化学习中的理解

在强化学习的背景下（例如贝尔曼期望方程），这两个式子都用来计算从状态 $s$ 出发并遵循策略 $\pi$ 时，下一个状态的期望价值。

第二个式子（更直观）：
- 内部 ( … )：计算在状态 $s$ 采取某个特定动作 $a$ 后，能转移到的下一个状态 $s’$ 的期望价值。
- 外部 $\sum_{a \in A} \pi(a|s) \dots$：因为你遵循策略 $\pi$，你会在 $s$ 处以 $\pi(a|s)$ 的概率选择动作 $a$。所以你用这个概率对所有可能的动作 $a$ 带来的期望价值进行加权平均。
第一个式子（数学等价）：
- 内部 ( … )：计算从状态 $s$ 出发，最终转移到某个特定下一个状态 $s’$ 的总概率。这需要遍历所有可能导致 $s’$ 的动作 $a$，并将它们的路径概率（$\pi(a|s) \times p(s’|s, a)$）相加。
- 外部 $\sum_{s’ \in S} v_\pi(s’) \dots$：用每个可能的下一个状态 $s’$ 的价值 $v_\pi(s’)$ 乘以你到达它的总概率，然后把所有 $s’$ 的结果加起来。

Examples for illustrating the Bellman equation

具体的代入方法：

Matrix-vector form of the BOE

和标量形式的联系：

$[f(v)]_s = \mathrm{max}_\pi \sum_{a} \pi(a|s) q(s, a), s \in S$

Contraction mapping theorem

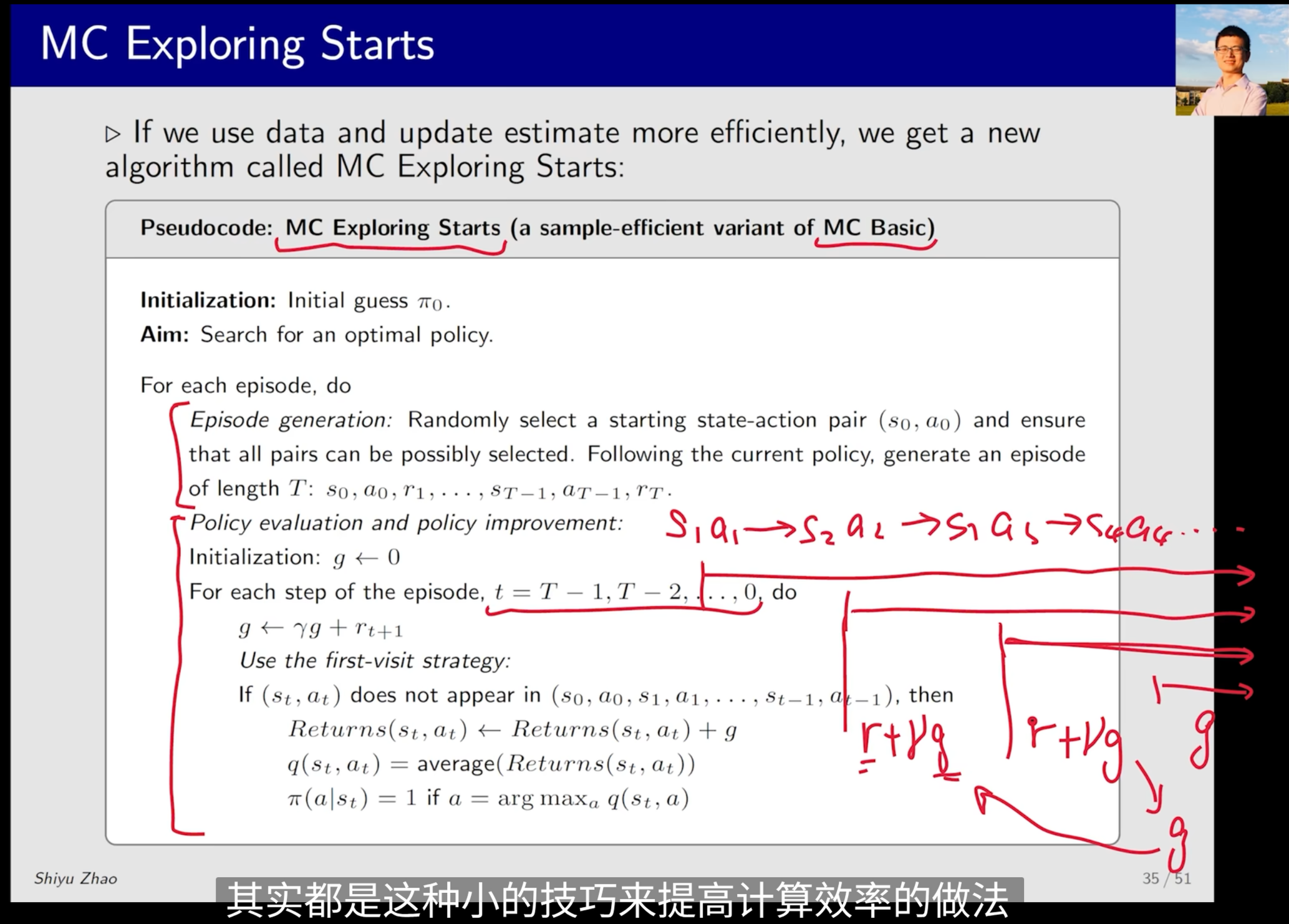
Updating policies more efficiently

Temporal-Difference Methods

一些引入的例子：

Off-policy vs on-policy

Deep Q-learning

原文中的神经网络（下）和简化版本（上）对比：

Policy Gradient Methods - Gradients of the metrics

具体的推导参考书中过程。

Actor-Critic Methods - The off-policy policy gradient theorem

这里不是 $\pi$，而是 $\beta$，它是一个固定的值。所以这里就没有什么探索，就是充分的利用。分母是不可变的。

DQN 代码实践

ref:

从 TensorFlow (TF) 转到 PyTorch 时，最不适应的往往就是Tensor 形状的显式管理。TF（特别是 Keras）常常会在后台自动处理维度对齐，而 PyTorch 则要求你对每一层的数据流动的形状（Shape）有非常清晰的掌控，尤其是在处理 Batch 维度和计算 Loss 的时候。

网络定义阶段 (Qnet 类)

在 CartPole-v0 环境中，状态（State）是连续变量，动作（Action）是离散的。

输入层：state_dim = 4 (位置, 速度, 角度, 角速度)。
输出层：action_dim = 2 (向左, 向右)。

class Qnet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        # PyTorch 的 Linear 层定义： (输入特征数, 输出特征数)
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim) 
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        # 假设输入 x 是一个 Batch 的数据
        # x.shape: [Batch_Size, 4]
        
        x = F.relu(self.fc1(x))  
        # fc1 输出 shape: [Batch_Size, 128]
        
        return self.fc2(x)
        # fc2 输出 shape: [Batch_Size, 2]
        # 这里的 2 代表对应动作 0 和动作 1 的 Q 值

收集经验与采样 (`ReplayBuffer` 与 `take_action`)

单样本处理 (`take_action`)

在与环境交互时，我们一次只处理一个状态。但是 PyTorch 的层通常期望输入带有 Batch 维度。

def take_action(self, state):
    # state 原始形状: numpy array (4,) -> [p, v, a, av]
    
    # 1. 增加 Batch 维度
    # torch.tensor([state]) 会把 (4,) 变成 (1, 4)
    state = torch.tensor([state], dtype=torch.float).to(self.device)
    # state.shape 现在是 [1, 4]
    
    # 2. 前向传播
    # self.q_net(state) 输出 shape: [1, 2] -> [[Q_action0, Q_action1]]
    
    # 3. 获取最大值的索引
    # .argmax() 返回最大值的索引 (0 或 1)
    # .item() 将单元素 Tensor 转换为 Python 标量 (int)
    action = self.q_net(state).argmax().item()
    return action

批量采样 (`ReplayBuffer.sample`)

当 update 被调用时，我们从 Buffer 中采样出一个 Batch（代码中 batch_size=64）。此时数据的形状如下（均为 numpy array）：

state: (64, 4)
action: (64,) (注意这里通常是一维数组)
reward: (64,)
next_state: (64, 4)
done: (64,)

核心训练逻辑 (`DQN.update`)

形状变化的重灾区。这是最容易通过不了编译或算错的地方。我们逐行拆解 update 函数中的 Tensor 变换。

数据预处理与维度调整

PyTorch 计算 Loss 时，通常要求维度严格匹配。

# 原始 transition_dict['actions'] 是一个 list 或 numpy array，shape 为 (64,)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
# .view(-1, 1) 等同于 TF 中的 .reshape(-1, 1)
# 变换后 actions.shape: [64, 1]
# 看起来像: [[0], [1], [0], ..., [1]]

rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
# rewards.shape: [64, 1]

dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
# dones.shape: [64, 1]

为什么要变成 [64, 1]？
因为后续计算 Q 目标值时，公式是 $R + \gamma \max Q$，如果不扩展维度，[64] 和 [64, 1] 相加可能会触发 PyTorch 的广播机制（Broadcasting），导致生成 [64, 64] 的矩阵，这是非常经典的错误。

计算当前状态的 Q 值 (`gather` 操作)

我们需要计算网络对当前状态下，实际采取的那个动作的 Q 值。

# 1. 计算所有动作的 Q 值
# states.shape: [64, 4]
q_values_all = self.q_net(states)  
# q_values_all.shape: [64, 2] -> 每个样本都有 [Q_left, Q_right]

# 2. 提取对应动作的 Q 值
# actions.shape: [64, 1] -> 存储了每个样本实际选了哪个动作的索引
q_values = q_values_all.gather(1, actions)
# .gather(dim=1, index=actions)
# 含义：在第 1 维（动作维），按照 actions 里的索引取值。
# 结果 q_values.shape: [64, 1]

gather 的直观理解： 假设 Batch=2：

Q_all = [[1.5, 2.0], [3.0, 1.0]] (形状 [2, 2])
Actions = [[1], [0]] (形状 [2, 1]，即第一个样本选了动作1，第二个选了动作0)
Result = [[2.0], [3.0]] (形状 [2, 1])

计算目标 Q 值 (`max` 操作)

我们需要计算下一个状态中，Q 值最大的那个动作对应的 Q 值（Target Q）。

# next_states.shape: [64, 4]
# self.target_q_net(next_states).shape: [64, 2]

# .max(1) 含义：在维度 1 上找最大值。
# 在 PyTorch 中，.max(dim) 会返回一个 namedtuple: (values, indices)
# [0] 取的是 values（最大 Q 值），[1] 取的是 indices（最大 Q 对应的动作）
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)

# 解释：
# .max(1)[0] 出来的 shape 是 [64] (一维)
# .view(-1, 1) 将其变成 [64, 1]
# 最终 max_next_q_values.shape: [64, 1]

PyTorch 的 tensor.max(dim) 同时返回数值和索引。

计算 TD Error 并反向传播

# 这里的加法和乘法都是 Element-wise 的
# rewards: [64, 1]
# max_next_q_values: [64, 1]
# dones: [64, 1]
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
# q_targets.shape: [64, 1]

# 计算 Loss
# q_values: [64, 1]
# q_targets: [64, 1]
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
# dqn_loss 是一个标量 (Scalar)

关于 CNN 部分 (`ConvolutionalQnet`)

代码最后附带了一个 CNN 网络，虽然在 CartPole 中没用到（CartPole 是向量输入），但如果是玩 Atari 游戏（图像输入），形状变化如下：

TF vs PyTorch 在图像上的区别：

TensorFlow: 默认 (Batch, Height, Width, Channel) -> NHWC
PyTorch: 默认 (Batch, Channel, Height, Width) -> NCHW

代码解读：

class ConvolutionalQnet(torch.nn.Module):
    def __init__(self, action_dim, in_channels=4):
        # ... 卷积层定义 ...
        # self.conv3 输出通道是 64
        
    def forward(self, x):
        # 假设输入图像是 84x84，堆叠 4 帧
        # x.shape: [Batch, 4, 84, 84]
        
        # 经过几层卷积和下采样（Stride）后
        # 假设最终特征图大小变为 7x7
        # x.shape: [Batch, 64, 7, 7]
        
        # 展平 (Flatten)
        # 这里的 view 等同于 Flatten
        # x.size(0) 是 Batch Size
        x = x.view(x.size(0), -1)
        # x.shape: [Batch, 64*7*7] -> [Batch, 3136]
        
        return self.head(x) 
        # 输出 [Batch, action_dim]

PyTorch 训练模型

关于：

dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
       dqn_loss.backward()  # 反向传播更新参数
       self.optimizer.step()

这部分在 tensorflow 中直接 model.fit() 就可以了，在 PyTorch 中则有所不同。

简单回答

TensorFlow 的 model.fit() 是一个高度封装的“全自动”函数，而 PyTorch 的这段代码则是把 model.fit() 内部的“黑盒子”拆开来，让用户手动控制每一步。

在 TensorFlow (Keras) 中，当你调用 model.fit() 时，它在每一个 Batch 内部其实悄悄干了这三件事：

步骤	PyTorch (手动挡)	TensorFlow Keras (自动挡 model.fit)	动作含义
1	`dqn_loss = ...`	(内部自动计算)	算错题：计算当前预测结果和真实结果的差距。
2	`optimizer.zero_grad()`	(内部自动执行)	清空草稿纸：把上一次计算的梯度清零（PyTorch 特有机制）。
3	`dqn_loss.backward()`	(内部自动执行)	找原因：反向传播，计算每个参数对误差的贡献（梯度）。
4	`optimizer.step()`	(内部自动执行)	改错题：根据梯度和学习率，更新网络权重。

详细拆解

`self.optimizer.zero_grad()` 清空梯度

“为什么要手动清零？难道不应该每次都是新的吗？”

这是 PyTorch 的一个独特设计机制：梯度累加 (Gradient Accumulation)。

默认行为：PyTorch 的 backward() 计算出的梯度，默认是累加到现有的梯度上的（grad += new_grad），而不是覆盖（grad = new_grad）。
如果不清零：你在第 1 个 Batch 算出的梯度，会和第 2 个 Batch 的梯度加在一起。用来更新权重时，方向就全乱了。
为什么这么设计？ 假设你的显存很小，只能跑 Batch Size = 4，但你想达到 Batch Size = 64 的训练效果。你可以：
1. 不调用 zero_grad。
2. 循环跑 16 次 backward()（累加梯度）。
3. 调用 1 次 step()。这就是“变相扩大 Batch Size”的技巧。

但在常规训练（如 DQN）中，我们不需要累加，所以必须手动告诉 PyTorch：“这一轮训练开始了，把上一轮的梯度记录清空！”

`dqn_loss.backward()` 反向传播

“这行代码在做什么？”

dqn_loss 是一个标量（Scalar，形状是 []）。
当你调用 .backward() 时，PyTorch 的自动微分引擎（Autograd）会从 dqn_loss 这个节点出发，沿着计算图往回走。
它会找到所有参与计算且 requires_grad=True 的权重参数（在 q_net 里），计算 loss 相对于这些参数的导数（梯度），并将结果存储在每个参数的 .grad 属性中。

`self.optimizer.step()` 参数更新

“这一步才是真正的学习。”

backward() 只是算出了梯度（告诉参数该往哪里变），但参数本身还没有变。
step() 会读取每个参数里的 .grad，并根据你设定的优化器算法（比如 Adam）和学习率（learning rate），执行下降操作 (注：Adam 的公式更复杂，但逻辑一致)： $\theta_{new} = \theta_{old} - \mathrm{lr} \times \nabla \theta$

在 TensorFlow 中写“手动挡”？

其实 TensorFlow 也有完全一样的写法，叫 tf.GradientTape。如果去看 TF 的高阶代码或自定义训练循环，会发现逻辑和 PyTorch 差不多。

这种手动挡的方式在强化学习（RL）中特别重要，因为 RL 的训练循环通常不是标准的 Epoch/Batch 结构，而是由环境交互驱动的，PyTorch 这种灵活性在 RL 领域非常受欢迎。

滑动平均

只是一个代码里面的小细节，记录一下。

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

这段代码实现了一个 保持输出长度不变（Same Length）的滑动平均（Moving Average） 算法。

在强化学习中，它通常被用来平滑（Smooth） 训练过程中的奖励（Reward）曲线，因为原始的 Reward 往往波动非常大，看不清趋势。

这段代码的写法非常“NumPy 风格”（向量化操作），比写 for 循环要快得多。为了呼应你对 向量/矩阵形状 的关注，我们把这段代码拆解成三部分来看：中间核心部分、开头部分 和 结尾部分。

假设：输入数组 a 的长度为 N，窗口大小 window_size 为 W（通常设为奇数）。

中间部分（核心逻辑）

1 2	cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size

这是计算滑动平均最高效的方法——积分图（Integral Image）技巧。

原理：如果不通过循环，怎么求数组中任意一段 [i, j] 的和？
- 先求前缀和 cumulative_sum（也就是累加值）。
- 区间 [i, j] 的和 = cumulative_sum[j+1] - cumulative_sum[i]。

形状变化：
- np.insert(a, 0, 0)：在 a 前面插入一个 0。形状从 (N,) 变为 (N+1,)。
- cumulative_sum：形状也是 (N+1,)。
- cumulative_sum[window_size:]：切掉了前 W 个，形状为 (N+1-W,)。
- cumulative_sum[:-window_size]：切掉了后 W 个，形状为 (N+1-W,)。
- 相减：形状对齐，直接相减。这步操作一次性算出了所有“完整窗口”的和。
- middle 的最终形状：(N - W + 1, )。

问题：如果只保留 middle，输出长度会比输入长度少 W-1 个点。为了画图时横坐标对齐，我们需要把两头“补”回来。

开头部分（边界处理）

1 2	r = np.arange(1, window_size-1, 2) begin = np.cumsum(a[:window_size-1])[::2] / r

当窗口在数组最左边滑动时，左边没有数据了。普通的做法是补 0（Padding），但这样会让平均值被拉低。这里的做法是：缩小窗口。

逻辑：
- 第 1 个点：用窗口大小 1 计算平均。
- 第 2 个点：用窗口大小 3 计算平均。
- … 直到窗口能扩张到 W 为止。
形状与细节：
- r：分母数组 [1, 3, 5, ..., W-2]。
- a[:window_size-1]：取前 W-1 个元素。
- np.cumsum(...)：前缀和。
- [::2]：关键切片。每隔一个取一个数（对应取索引 0, 2, 4…）。这正好对应了累加 1 个数、累加 3 个数、累加 5 个数的和。
- begin 的最终形状：( (W-1)/2, ) （假设 W 是奇数）。

结尾部分（边界处理）

1	end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]

和开头部分的逻辑完全对称：

先用 [::-1] 把数组倒序。
用同样的逻辑计算变长平均。
最后再用 [::-1] 把结果倒回来。
end 的最终形状：( (W-1)/2, )。

总结：形状拼接

最后一步 np.concatenate 将这三部分拼起来：

$\text{Length} = \underbrace{\dfrac{W-1}{2}}_{\text{begin}} + \underbrace{(N - W + 1)}_{\text{middle}} + \underbrace{\dfrac{W-1}{2}}_{\text{end}} = N$

结论：
这段代码的作用是 对输入序列 a 进行平滑处理，且保证输出序列的长度（Shape）与输入完全一致 (N,)。

为什么你要懂这个？
在 Deep Learning 代码中，你经常会在 train 结束后看到类似这样的调用：

1
2
3

# return_list 是每个 episode 的奖励，波动剧烈
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return) # 绘制平滑后的曲线

如果你不处理边界（只用 middle），episodes_list 和 mv_return 的长度就会不匹配（差了8个点），Matplotlib 就会报错 x and y must have same first dimension。这段代码就是为了解决这个形状对齐问题的。

Double DQN

ref:

原理

链接中的解释有点晦涩，我提出自己的理解，但不能保证其正确性。

在 DQN 中，在计算

$\max_{a \in \mathcal{A}(S')} \hat{q} (S', a, w_T)$

时，我们的做法是：

然后，做两件事：选择 value 最大的 action, 将它的值返回。

这会导致误差的积累。例如，Target Net 对 a2 作出了过高估计，由式 (8.38),

$R + \gamma \max_{a \in \mathcal{A}(S')} \hat{q} (S', a, w_T)$

会被过高估计，因为我们旨在降低目标函数的值（should equal zero in the expectation sense），从而导致 $\hat{q}(S, A, w)$ 被过高估计。

这样的误差将会逐步累积。对于动作空间较大的任务，DQN 中的过高估计问题会非常严重，造成 DQN 无法有效工作的后果。

Double DQN 的解决方法是：
使用训练网络选取 action, 目标网络计算 value. 即，我们需要减少

$\color{green}{ R + \gamma \hat{q}(S', \underset{a \in \mathcal{A}(S')}{\mathrm{argmax}}\hat{q}(S',a, w), w_T) }$

与 $\color{green}{\hat{q}(S, A, w)}$ 的差距。

这些误差是由神经网络本身带来的，Double DQN 并不能避免误差，但是这两个网络的误差“方向”可能不一样。

但是这在理论上带来了新的问题，式 (8.38) 是 $J$ 对 $w$ 求导，在原来的

$R + \gamma \max_{a \in \mathcal{A}(S')} \hat{q} (S', a, w_T)$

中，不包含 $w$. Double DQN 却引入了 $w$, 在求导的时候会带来困难。

关于“梯度求导”的理论担忧，在深度强化学习的实际操作（Semi-gradient 方法）中，这个问题的处理方式比较“简单粗暴”。

数学与工程实现的解释：
1. Semi-gradient (半梯度) 方法：在 Q-learning 及其变体（包括 DQN）中，我们使用的是半梯度方法。这意味着，在计算梯度时，我们强制将目标值 $Y$ 视为常数（Constant）。
  - 即使 $Y$ 的计算过程用到了 $w$（用来选动作），我们在反向传播时，会切断这部分的梯度流。
  - 这正如书中所说：“For the sake of simplicity, it is assumed that the value of $w$ in $y$ is fixed”。这个假设在 Double DQN 中依然适用。
2. Argmax 的不可导性：从数学角度看，$\text{argmax}$ 操作本身是离散的、分段常数的（Step function）。在绝大多数点上，$\text{argmax}$ 的导数为 0；在跳变点上，导数未定义。因此，即使想对它求导，梯度也传不回去。
3. 理解为“噪声”？：“是否可以简单理解为引入了一种噪声”？
  - 这不完全准确。它不是随机噪声，而是一种去偏（De-biasing）机制。
  - 与其说是噪声，不如说是 “交叉验证”。我们在用网络 A 告诉我们“谁是第一名”，然后问网络 B “第一名考了多少分”。这打破了“自卖自夸”（用网络 A 选第一名，又用网络 A 打分）带来的正向偏差循环。

部分代码细节

def dis_to_con(discrete_action, env, action_dim):  # 离散动作转回连续的函数
    action_lowbound = env.action_space.low[0]  # 连续动作的最小值
    action_upbound = env.action_space.high[0]  # 连续动作的最大值
    return action_lowbound + (discrete_action /
                              (action_dim - 1)) * (action_upbound -
                                                   action_lowbound)

这段代码用于解决 DQN 只能处理离散动作 与 倒立摆环境（Pendulum-v0）需要连续动作 之间的矛盾。

它本质上是一个 线性插值（Linear Interpolation） 函数，将神经网络输出的离散索引（如 0, 1, 2…）映射回环境实际需要的连续物理数值（如力矩 -2.0, -1.6…）。

环境限制：Pendulum-v0 环境的动作是一个连续的力矩值，范围是 $[-2.0, 2.0]$ 。
算法限制：DQN 算法只能输出离散的动作编号（即选择第几个动作）。
解决方案：将连续的动作空间“切分”成若干份（文中设为 action_dim = 11），用离散的编号 0 到 10 来代表这些切分点。

def dis_to_con(discrete_action, env, action_dim):
    # 获取环境动作空间的下界（最小值）。
    # 在 Pendulum-v0 中，这个值是 -2.0
    action_lowbound = env.action_space.low[0]
    
    # 获取环境动作空间的上界（最大值）。
    # 在 Pendulum-v0 中，这个值是 2.0
    action_upbound = env.action_space.high[0]
    
    # 核心公式：线性映射
    return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)

这个返回值的计算公式可以理解为：

$\text{实际动作} = \text{最小值} + \text{比例} \times \text{总跨度}$

总跨度 (action_upbound - action_lowbound)：即 $2.0 - (-2.0) = 4.0$ 。这是动作值的变动总范围。
比例 (discrete_action / (action_dim - 1))：
- discrete_action 是当前神经网络选出的动作编号（例如 0, 5, 10）。
- action_dim - 1 是最大的动作编号（因为编号从0开始，11个动作的最大编号是 10）。
- 这个部分计算当前动作在所有动作中排在什么位置（百分比）。例如，编号 0 对应 0%，编号 5 对应 50%，编号 10 对应 100%。